SatNOGS Rotator v3
| SatNOGS Rotator v3 | |
|---|---|
| Rotator Information | |
| Type: | Az/El |
| Cost: | ~200 USD |
| Release Information | |
| Status: | Beta |
| Latest Release: | Torx Flathead (v3.0.1) |
| Repository: | [1] |
| Documentation: | [2] |
Contents
Intro
v3 marks a major re-haul of the SatNOGS Rotator design, with learnings from v2 applied. You can see a lot of the thinking and background research that was conducted prior to v3 development in this thread.
Also in this list is presented different rotators, either commercial or DIY builds.
Specifications
| SatNOGS v3 Rotator | |
| Plastic Parts | 26 |
| Non Printed Parts approx. | 345 |
| Cost | ~ $220 |
| Controller Electronics | SatNOGS Rotator Controller |
| Type | AZ/EL (possible X/Y) |
| Motors | 2x NEMA 17 Stepper or 2x DC Motors |
| Frame Material | Aluminum T-slot 20x20 |
| Speed (deg/sec) | ? (Stepper motor), ? (DC motor) |
| Torque (Nm) | ~? (Stepper motor), ~? (DC motor) |
| Brake Torque (Nm) | ? |
| Dimensions (mm) | 306.5x197x142.5 (AZ/EL) |
| Weight (kg) | 6.2 |
| Pro | |
| Con | |
Brake Torque
The greatest force the tracker needs to withstand is the force created by strong wind. The worst case is when one antenna is elevated at 90 degs, facing the direction of the wind. We based our calculations on an article found online after comparing it to others. We “translated” the second table in metric (because we don’t understand imperial and because we needed same units system in our calculations)
| Method | Wind Zone(km/h) | Height (m) | Pressure(N/m^2) |
|---|---|---|---|
| EIA-222-C | 160 | N/A | 1280 |
| EIA-222-F | 128 | 14 | 1260 |
| EIA-222-F | 128 | 21 | 1390 |
| EIA-222-F | 128 | 30 | 1500 |
| UBC'97 | 128 | 14 | 1290 |
| UBC'97 | 128 | 21 | 1160 |
| UBC'97 | 128 | 21 | 1390 |
| UBC'97 | 128 | 30 | 1260 |
| UBC'97 | 128 | 42 | 990 |
| UBC'97 | 128 | 42 | 1360 |
| Generic Formula | 150 | N/A | 1270 |
and we applied the worst case model (EIA-222-F) in 3 different antennas: in the biggest one of our designs, and in two others, for which we obtained data from yaesu G800 rotator manual at page 3. We assumed that antennas are mounted in 1m away from the azimuth axis. For our antenna with 2m length (actual, not wavelength), made by 2cm square tube, the generated torque was ≈600Kg*cm. For the 144MHz 10-elements Yagi from the article is ≈6000Kg*cm and for the third 430MHz, 12-elements Yagi is ≈1800Kg*cm
Moment of inertia
Now for the moment of inertia: (for all installation methods we assumed that antennas are counterbalanced in the elevation axis) the worst case scenario here is to use two 3kg (our designs are less than 1kg) back mounted yagis with 3kg counterbalances both mounted in 0.75m away from azimuth axis. The torque you need in order to accelerate this system from ω=0deg/s angular velocity to ω=5deg/s (the math about angular velocity is below) in one second is about 60kg*cm.
Note: we suppose that the mass of antennas is near to the altitude axis, so the torque of this axis that is needed to accelerate is approximately 0.
- M1: torque of Azimuth axis
- L: length of center of mass of antennas from azimuth axis (0.75m)
- m: mass of antennas and of counterweight (3kg + 3kg = 6kg)
- I: moment inertia
- a: angular acceleration of azimuth axis 5deg/s^2
- I = I1 + I2 = m*L^2 + m*L^2 = 2*m*L^2 = 6.75 kg*m^2
- M1 = I*a = 6.75kgm^2 * 0.087rad/s^2 = 0.58 Nm = 5.8 kgm = 58 kgcm
Angular velocity
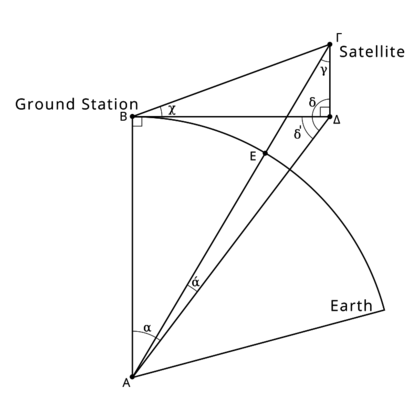
(How well do you remember trigonometry?)For the angular velocity max needed in altitude axis the things are straightforward. The closer is the satellite the larger the velocity. According to the wikipedia article about LEO, the lowest height limit is 160 km and the speed unit to orbit earth in this altitude is 7,8 km/s. As a result, maximum velocity in ALT axis is 2,8 deg/s. In ALT AZ rotator design there is a well known limitation: the closer something passes near zenith the biggest gets the velocity of the AZ axis. Therefore, we have analyzed this problem to figure out the optimal velocity and how high we are allowed to track a target in relation to AZ velocity. The picture below illustrates a ground station B which tracks a satellite Γ in X degrees altitude. The satellite velocity at this point is vertical to the screen (page) plane.
The equations that lead to maximum altitude at which we can track in relation to AZ angular velocity are
- ω : angular velocity of AZ DOF in rad/s
- H = ΑΕ + ΕΓ : Minimum Height of LEO, 160 km
- R = ΑΕ : Radius of Earth, 6500 km
- u : linear velocity of satellite that rotates in 160km height is 7.8 km/s
- ΒΔ = u / ω : ΒΔ in km
- α = atan(ΒΔ / R)
- δ = π - α
- γ = asin( sqrt(R^2+ΒΔ^2) * sin(δ) / (H+R) )
- ά = π - δ - γ
- ΓΔ = (H+R) * sin(ά) / sin(δ)
- χ = atan(ΓΔ / ΒΔ)
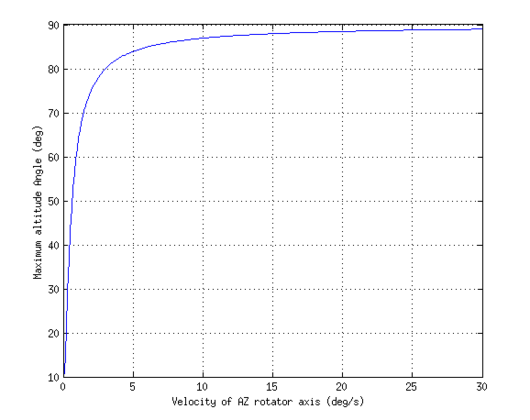
Below you can see the plot of the equations mentioned above, where horizontal axis represents angular velocity (ω) in deg/s and vertical axis shows the max track altitude (χ) for lower bound of LEO.
After studying this diagram, we came up to the conclusion that an angular velocity of 5 deg/s is adequate. For this decision, we took into consideration the main lobe of antenna (Δ3db) which in most situations is about 20 deg.
General Specifications
Together with the above mentioned specifications, we would also like for the 3rd version of SatNOGS rotator to be:
- inexpensive (less than €300, if possible)
- lightweight and portable (~6Kg, size:~300x~150x~150mm)
- rigid and durable
- easy to build and fix (try to use easily available materials)
- weatherproof
- electromagnetically shielded, so that noise in reception is reduced
- accurate (<1deg, backslash reduction and use of encoders at the axis)
Sourcing
3d Printing at a Fab Lab or your local hackerspace: If you don't have your own 3d printer, then a local Fab Lab or hackerspace may be able to do it for you. Fab Labs and hackerspaces are places that have invested in the machinery and you can take the designs to them. Generally they need .stl files to import into the software that runs the machines, but this should be discussed with the Fab Lab or hackerspace. You then pay for the material, time or a combination of the two for each of the parts or any other agreement in place.
Most people building the rotator have had success builds with simple ABS material for the 3D printing parts.
T Slot - If you don't want to cut the pieces yourself, then you may be able to find a supplier that will do this for you. (Here's one in the United Kingdom.)
Hidden corner connectors - AliExpress gave the cheapest supplier
A good US source is MISUMI-USA; they will also cut to length. MISUMI has several other global locations [3].
Beware, the 20-series T-slot from 80/20 Inc. in the US has slots that are only 5.2mm wide. The hidden corner connectors from e.g. AliExpress will not fit.
Stepper Motors - eBay
Belts - eBay
Fixings / Pipe - eBay
Build Sequence
- Make sure you have all parts
- Follow the instructions for mechanical assembly
- Once mechanical assembly is ready, construct the SatNOGS Rotator Controller and connect it to the assembly.
- You are ready! Proceed with testing.
Worm Gear Box Calculations
- Gear ratio: i12 = 30
- Angle between axis of gears: δ = 90 deg
- Number of threads in worm: If i12 >= 30 then z1 = 1
- Number of teeth in worm wheel: z2 = i12*z1 = 30
- Center distance: initial case a = 45.5 mm
- Worm reference diameter: AGMA d01>= 11.5*(a/25.4)^0.875 = 19.15 mm, so d01 = 19.5mm
- Worm wheel reference: d02 = 2*a - d01 = 71.5 mm
- Axial module: ms = d02/z2 = 2.38 , so ms = 2.5
Recalculate d02, a with new axial module
- d02 = z2*ms = 75mm, a = (d02+d01)/2 = 47.25mm
- Axial pitch: ts = π*ms = 7.854mm
- Reference lead angle: γ0 = atan(d02/(i12*d01)) = 7.3 deg
- Worm tip diameter: dk1 = d01 + 2*hk = 24.5mm
- Worm teeth reference addendum in axial section: hk = hk* *ms = 2.5mm
- Worm tooth reference addendum coefficient: hk* = 1
- Worm root diameter: df1 = d01 - 2*hf = 13.5mm
- Worm tooth reference dedendum: hf = hf* _ms = 1.2_ms = 3mm
- Dedendum coefficient: hf* = 1.2
- Worm length: L = 2.5_ms_sqrt(z2+2) = 35.36mm
- Worm tooth thickness: smx1 = smx1* * ts = 3.927mm
- Tooth thickness coefficient: smx1* = 0.5
- Normal pressure angle: aon = 20 deg
- Worm wheel throat diameter: dk2 = d02+2*hk = 80mm
- Worm wheel root diameter: df2 = d02 - 2*hf = 69mm
- Worm wheel outside diameter: de2 = dk2 + 2*mx = 83.5mm
- Worm wheel tooth external addendum: mx = n*ms, 0.4<=n<=1.5
- Effective worm wheel face width: b2H,max = sqrt((2_a - df2)^2 - (2_a - de2)^2) = 23mm
Test Sequence
Test sequence needed